jueves, 27 de septiembre de 2012
miércoles, 26 de septiembre de 2012
Operaciones básicas
| Una de las cosas imprescindibles en matemáticas y lo que nos va a servir para todas las operaciones que realicemos en el futuro, es comprender que todo número lleva siempre consigo un signo, ya sea positivo o negativo. Cuando nos encontremos con un número sin signo (por ejemplo 6), debemos saber que para aplicarlo a cualquier operación es como si estuvieramos ante un +6. |
| LOS SIGNOS NEGATIVOS (-) Y POSITIVOS (+)TAMBIEN SE SUMAN, RESTAN, MULTIPLICAN Y DIVIDEN |
| SUMA Y RESTA DE SIGNOS |
Cuando nos encontramos con operaciones de suma y resta de números con distintos signos, la norma a seguir siempre es la siguiente: SE SUMAN SIEMPRE todos los números que tengan el mismo signo, ya sea + o - y el resultado mantendrá el mismo signo. Parece lógico, si tu tienes una deuda de 2 euros (-2) y otra de 3 euros (-3), el total será la suma de las cantidades manteniendo el signo negativo (-5) Si por el contrario, tienes 2 euros (+2) y 3 euros (+3), el resultado será también la suma de los números, pero con su signo correspondiente (+5), aunque recordemos que cuando un número es positivo, podemos suprimir el signo + ya que se da por supuesto. Ahora bien, si lo que nos plantean son números de signo diferente, SIEMPRE SE RESTARAN las cantidades, y el resultado tendrá el signo del mayor. Si debemos 5 euros (-5) y tenemos 3 euros (+3), el resultado sera la diferencia entre los numeros con el signo del mayor, (-2) Esta operación nos la podemos encontrar de dos formas: 3-5 = -2 o bien -5 + 3 = - 2 En ambos casos el resultado es el mismo. La complicación puede venir cuando nos presentan una serie de operaciones con diferentes signos: -2+3-6+1-9-3+5+7 En este caso, sumaremos todos los números con signo - -2-6-9-3= -20 (-2 mas -6 mas -9 mas -3 = -20) Y todos los que tengan signo + 3+1+5+7= 16 Finalmente restaremos las cantidades resultantes (ya que siempre que tengan signos distintos se restan) y mantendremos el signo del mayor. -20 + 16 = -4 |
| MULTIPLICACION Y DIVISION DE SIGNOS |
| Para multiplicar o dividir números con igual o distinto signo, debemos aprender la siguiente regla: + x + = + + x - = - - x + = - - x - = + Podemos resumirlo en que la multiplicación de dos números con el mismo signo (da igual que sea - o +) siempre da como resultado un número positivo (+), mientras que la multiplicación de números con signo diferente siempre da como resultado un número negativo (-) En la división pasa exactamente lo mismo: + : + = + + : - = - - : + = - - : - = + |
REGLETAS DE CUISENAIRE
Las regletas Cuissenaire son un material matemático destinado básicamente a que los niños aprendan la composición y descomposición de los números e iniciarles en las actividades de cálculo, todo ello sobre una base manipulativa. El material consta de un conjunto de regletas de madera de diez tamaños y colores diferentes. La longitud de las mismas va de 1 a 10 cm. Cada regleta equivale a un número determinado:
- La regleta blanca, con 1 cm. de longitud, representa al número 1.
- La regleta roja, con 2 cm. representa al número 2.
- La regleta verde claro, con 3 cm. representa al número 3.
- La regleta rosa, con 4 cm. representa al número 4.
- La regleta amarilla, con 5 cm. representa al número 5.
- La regleta verde oscuro, con 6 cm. representa al número 6.
- La regleta negra, con 7 cm. representa al número 7.
- La regleta marrón, con 8 cm. representa al número 8.
- La regleta azul, con 9 cm. representa al número 9.
- La regleta naranja, con 10 cm. representa al número 10.
Objetivos a conseguir:
- Asociar la longitud con el color.
- Establecer equivalencias.
- Formar la serie de numeración de 1 a 10.
- Comprobar la relación de inclusión de la serie numérica.
- Trabajar manipulativamente las relaciones “mayor que”, “menor que” de los números basándose en la comparación de longitudes.
- Realizar diferentes seriaciones.
- Introducir la composición y descomposición de números.
- Iniciar las operaciones suma y resta de forma manipulativa.
- Comprobar empíricamente las propiedades conmutativa y asociativa de la suma.
- Iniciarlos en los conceptos doble y mitad.
- Realizar repartos.
martes, 25 de septiembre de 2012
Scracht
ACTIVIDAD DE DIALOGOS CON SCRACHT
Con esta actividad se pretende que los estudiantes desarrollen su habilidad para crear historias interactivas; para ello crearán un diálogo entre dos personajes utilizando Scratch.
La tarea debe realizarse en dos partes. Primero, representarán la comunicación entre dos personajes mediante la reproducción de una tira cómica impresa. Después, los estudiantes crearán un diálogo entre dos personajes, en el que se vea la secuencia de este, para lo cual deberán sincronizar la acción (manejo de tiempos de espera). En esta segunda parte se debe incluir movimiento o algún tipo de animación (cambio de disfraz, etc.) a los personajes.
Objetivos:
Al finalizar esta actividad los estudiantes estarán en capacidad de:
- Utilizar las instrucciones "decir" y "pensar" para representar la interacción entre dos personajes en una sola imagen fija (como en una tira cómica).
- Dar ubicación inicial a un objeto (coordenadas x,y)
- Dar dirección de desplazamiento a un objeto
- Mover un objeto de un lugar a otro, incorporando cambios de disfraz e instrucciones repetitivas
- Utilizar instrucciones "decir por N segundos" o "pensar por N segundos", "esperar" o algunas similares, que permitan lograr una adecuada sincronización en el diálogo de los dos personajes.
- Agregar un fondo musical a la animación
- Agregar un sonido a un objeto, que se ejecute en algún o algunos momentos durante la animación.
- Cambiar el fondo del escenario
viernes, 7 de septiembre de 2012
jueves, 6 de septiembre de 2012
ÁNGULOS
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. los Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.y Un ángulo recto es aquel que mide 90°. Su amplitud medida en otras unidades es: π/2 radiales y 100g (centesimales). Sus dos lados son dos semirrectas perpendiculares, y el vértice es el origen de dichas semirrectas.

Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. los Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.y Un ángulo recto es aquel que mide 90°. Su amplitud medida en otras unidades es: π/2 radiales y 100g (centesimales). Sus dos lados son dos semirrectas perpendiculares, y el vértice es el origen de dichas semirrectas.
CLASIFICACIÓN DE LOS ÁNGULOS
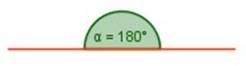
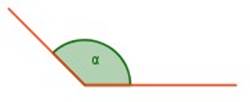
Los ángulos pueden clasificarse según su medida en cinco tipos:
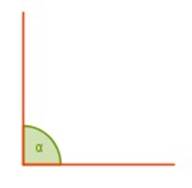
Ángulo recto: es aquel cuya medida es de 90°
∠ α = 90°
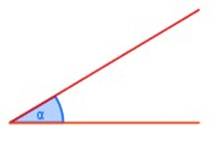
Ángulo agudo: es aquel cuya medida es menor que 90°
∠ α = < 90°
Los bloques lógicos constan de cuarenta y ocho piezas sólidas, de madera o plástico de fácil manipulación. Cada pieza se define por cuatro variables: color, forma, tamaño y grosor. Cada una tiene unos valores:
El color: rojo, azul y amarillo.
La forma: cuadrado, círculo, triángulo y rectángulo.
El tamaño: grande y pequeño.
El grosor: grueso y delgado.
utilidad
Sirven para poner a los niños ante unas situaciones que les permitan llegar a determinados conceptos matemáticos. A partir de las actividades los niños llegan a:
Nombrar y reconocer cada bloque.
Reconocer las variables y valores de éstos.
Clasificarlos atendiendo a un solo criterio.
Comparar los bloques estableciendo semejanzas y diferencias.
Realizar seriaciones siguiendo unas reglas.
Establecer la relación de pertenencia a conjuntos.
Emplear los conectivos lógicos (conjunción, negación, disyunción, implicación).
Definir elementos por la negación.
Introducir el concepto de número.
jueves, 30 de agosto de 2012
lógica matemática
conjuntos
La palabra conjunto generalmente la asociamos con la idea de agrupar objetos, por ejemplo un conjunto de discos, de libros, de plantas de cultivo y en otras ocasiones en palabras como hato, rebaño, piara, parcelas, campesinado, familia, etc., es decir la palabra conjunto denota una colección de elementos claramente entre sí, que guardan alguna característica en común. Ya sean números, personas, figuras, ideas y conceptos.
En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:
{ a, b, c, ..., x, y, z}
Como se muestra el conjunto se escribe entre llaves ({}) , o separados por comas (,).
OPERACIONES CON CONJUNTOS
UNION
La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:
A È B = { x/x Î A ó x Î B }
Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }
A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }
INTERSECCION
Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }
Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:
A Ç B = { x/x Î A y x Î B }
Y se lee el conjunto de elementos x que están en A y están en B.
Ejemplo:
Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }
Q Ç P={ a, b, o, r, s, y }
CONJUNTO VACIO
Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .
Por ejemplo:
Sean A={ 2, 4, 6 } y B={ 1, 3, 5, 7 } encontrar A Ç B.
A Ç B= { }
El resultado de A Ç B= { } muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:
A Ç B=Æ
CONJUNTOS AJENOS
Sí la intersección de dos conjuntos es igual al conjunto vacío, entonces a estos conjuntos les llamaremos conjuntos ajenos, es decir:
Si A Ç B = Æ entonces A y B son ajenos.
COMPLEMENTO
El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprehensión como:
A'={ x Î U/x y x Ï A }
Ejemplo:
Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
A= { 1, 3, 5, 7, 9 } donde A Ì U
El complemento de A estará dado por:
A'= { 2, 4, 6, 8 }
DIFERENCIA
Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:
A - B={ x/x Î A ; X Ï B }
Ejemplo:
Sea A= { a, b, c, d } y
B= { a, b, c, g, h, i }
A - B= { d }
En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es
B – A = { g, h, i }
E indica los elementos que están en B y no en A.
DIAGRAMAS DE VENN
Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.Esencialmente, se conoce al diagrama de Venn como una forma de mostrar de manera gráfica, una agrupación de elementos según los conjuntos, siendo representado cada conjunto con una circunferencia. Esta clase de gráficos se emplean en la Teoría de Conjuntos, dentro de las matemáticas modernas y nos explica el funcionamiento de un conjunto de elementos al realizar alguna operación con ellos.
La manera de representar el conjunto Universal es un rectángulo, ó bien la hoja de papel con que se trabaje.
Un ejemplo de la representación del conjunto universal se muestra como:
tabla de verdad
Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921
conjuntos
En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:
La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:
A È B = { x/x Î A ó x Î B }
Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }
A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }
Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }
Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:
A Ç B = { x/x Î A y x Î B }
Y se lee el conjunto de elementos x que están en A y están en B.
Ejemplo:
Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }
Q Ç P={ a, b, o, r, s, y }
Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .
Por ejemplo:
Sean A={ 2, 4, 6 } y B={ 1, 3, 5, 7 } encontrar A Ç B.
A Ç B= { }
El resultado de A Ç B= { } muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:
A Ç B=Æ
Sí la intersección de dos conjuntos es igual al conjunto vacío, entonces a estos conjuntos les llamaremos conjuntos ajenos, es decir:
Si A Ç B = Æ entonces A y B son ajenos.
El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprehensión como:
A'={ x Î U/x y x Ï A }
Ejemplo:
Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
A= { 1, 3, 5, 7, 9 } donde A Ì U
El complemento de A estará dado por:
A'= { 2, 4, 6, 8 }
DIFERENCIA
Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:
A - B={ x/x Î A ; X Ï B }
Ejemplo:
Sea A= { a, b, c, d } y
B= { a, b, c, g, h, i }
A - B= { d }
En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es
B – A = { g, h, i }
E indica los elementos que están en B y no en A.
Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.Esencialmente, se conoce al diagrama de Venn como una forma de mostrar de manera gráfica, una agrupación de elementos según los conjuntos, siendo representado cada conjunto con una circunferencia. Esta clase de gráficos se emplean en la Teoría de Conjuntos, dentro de las matemáticas modernas y nos explica el funcionamiento de un conjunto de elementos al realizar alguna operación con ellos.
La manera de representar el conjunto Universal es un rectángulo, ó bien la hoja de papel con que se trabaje.
Un ejemplo de la representación del conjunto universal se muestra como:
tabla de verdad
Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921
valor verdadero
El valor verdadero se representa con la letra V, si se emplea notación numérica se expresa con un uno: 1, en un circuito eléctrico, el circuito esta cerrado.
valor falso
El valor falso se representa con la letra F, si se emplea notación numérica se expresa con un cero: 0, en un circuito eléctrico, el circuito esta abierto
variables
Para una variable lógica A, B, C, ... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:
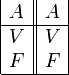
- La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

- conjunciones
- La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderasLa tabla de verdad de la conjunción es la siguiente:

- disyunciones
- La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.La tabla de verdad de la disyunción es la siguiente:

Implicación o Condicional
El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa, yverdadero en cualquier otro caso.La tabla de verdad del condicional material es la siguiente:
Bicondicional
El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.La tabla de verdad del bicondicional es la siguiente: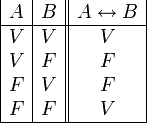
Suscribirse a:
Entradas (Atom)